스칼라함수는 앞에서 말한 온도장, 기압장 등에 활용이 됩니다. 하지만 온도장, 기압장 등이 항상 일정하라는 법은 없습니다. 이와 같이 함수의 변화율을 나타내기 위해서 스칼라장의 기울기를 구해서 표현합니다. 즉 기울기는 스칼라장으로부터 벡터장을 얻을 수 있습니다.
- 기울기 정의

다음은 미분연산자 $\nabla$ ( nabla ) 입니다.

3차원 공간에서 스칼라 함수 $f$가 미분가능할 때, 스칼라 함수의 기울기는 grad $f$ ( ∇$f$ ) 로 표기합니다.
- 방향도함수

기울기의 정의에서 스칼라함수에 대하여 함수 $f$의 변화율을 표현했습니다. 이를 이용해서 공간에서의 $f$의 변화율을 찾을 수 있습니다.

방향도함수 $D_b~f$의 정의는 공간상의 점 $P$에서 벡터 $b$의 방향으로의 함수 $f$입니다. |b|=1인 단위벡터일 때, 직선 L은 다음과 같습니다.

$r(s)'=x'$i+$y'$j+$z'$k=b입니다. 따라서 b와 $grad ~f$의 내적이 됩니다.

- 법선벡터
$f$는 공간에서 미분가능한 스칼라함수이고, $f(x,y,z)$=c는 곡면을 나타낸다. 곡면위의 점P에서 $f$의 기울기가 0이 아닐 때 이 기울기는 점 P의 곡면에서의 법선벡터가 된다.
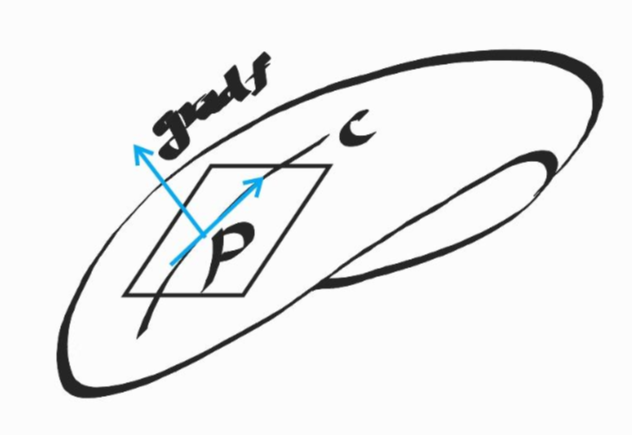
미분가능한 스칼라 함수 $f(x,y,z)=c$로 표현된 곡선에 대하여 그 위의 r($t$) = [$x(t), ~y(t),~z(t)$]로 표현됩니다. 점 P에서의 접선벡터들은 접평면을 이루고, 이 접평면에 수직인 벡터는 $grad~f$입니다.
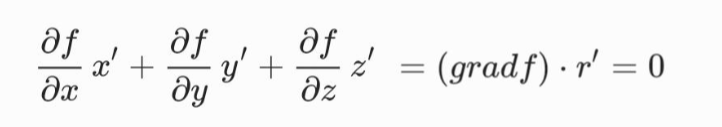
위의 식에 의해서 접평면과 $grad~f$가 수직한다는 것을 알 수 있습니다.
'수학 (Mathematics) > 공업 수학 (Advanced Engineering Mathematics)' 카테고리의 다른 글
| 벡터의 미적분 응용 (0) | 2020.03.13 |
|---|---|
| 벡터의 적분 ( integral ) (0) | 2020.03.12 |
| 벡터의 도함수 ( derivatives ) (0) | 2020.03.12 |
| 벡터의 외적 ( cross product ) (1) | 2020.03.11 |
| 벡터의 내적 (dot product) (0) | 2020.03.11 |




댓글