벡터에 대해 미분을 할 수 있으면 반대인 적분도 할 수 있습니다. 이번에는 벡터의 적분에 필요한 기본지식들을 알아보고 실제 벡터에 대한 적분을 해보도록 하겠습니다.
“Give me a lever long enough and a fulcrum on which to place it, and I shall move the world. ”
- Archimedes -
적분 개념의 시초는 너무나도 유명한 일화인 순금왕관의 진위여부를 알아낸 아르키메데스로부터 시작되었습니다. 아르키메데스는 현재의 적분과 비슷한 방식으로 도형의 면적이나 구의 면적을 구했습니다. 하지만 이 시기까지만 해도 무한대 개념에 대한 정립이 되어있지 않아 적분에 대한 개념도 없었습니다. 이후 무한대의 개념이 정립되기 시작하면서 여러 학자들에 의해서 적분의 개념이 현재까지도 계속해서 발전해 나가고 있습니다.
- 기본 지식
- 매개변수 표현법
고교과정에서 배운 매개변수 표현법을 벡터에서도 동일하게 적용할 수 있습니다. 매개변수 표현법은 공학 등 다양한 미분기하학적 방법에 사용되기 때문에 잘 익혀놔야 합니다.
|
r(t) = [$x$($t$), $y$($t$), $z$($t$)] = $x$($t$)i + $y$($t$)j + $z$($t$)k 여기서 매개변수는 $t$이고 변수 $x$, $y$, $z$는 직교좌표를 나타냅니다. |
예시
① 직선

r(t) = a + tb = [$a_1$ + t$b_1$, $a_2$ + t$b_2$, $a_3$ + t$b_3$].
위치벡터 a의 종점 A를 지나고 상수벡터 b의 방향으로의 직선 L는 다음과 같이 표현됩니다.
② 원, 타원

r($t$) = [$acost$, $asint$] ( 0 ≤ $t$ ≤ 2$\pi$ )
중심이 원점이고 반지름이 $a$인 $xy$평면 위의 원 $x^2 + y^2 = a $ , $z$ = 0 에 대한 표현입니다.
r($t$) = [$acos t$, $bsin t$, 0] = $acos t$i + $bsin t$j ( 0 ≤ $t$ ≤ 2$\pi$ )
중심이 원점이고 주축이 $x$축과 $y$축인 $xy$평면위의 타원에 대한 표현입니다.
③ 뒤틀린 곡선 ( Circular Helix )
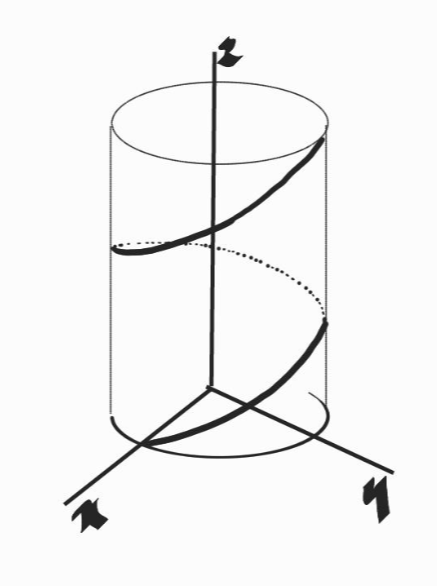
r($t$) = [$acos t$, $bsin t$, $ct$] = $acos t$i + $bsin t$j + ctk
$xy$평면에 대하여 반지름이 $a$인 원이고 $z$축에 대하여 매개변수 $t$에 따라 증가 또는 감소하는 형태입니다.
- 곡선의 접선

곡선 C가 r(t)로 표현이 가능하고, 점 P,Q가 t, t+△t에 대응될 때 △t를 0으로 극한을 취했을 때 직선은 점P로 점점 만나게 됩니다. 따라서 다음 벡터의 극한값은 아래 도함수가 됩니다.
$\lim_{\Delta t\rightarrow\infty}$$\frac{1}{\Delta~t}$[r(t+$\Delta$t) - r(t)]
다음과 같이 접선벡터를 구할 수 있다면 점 P에서의 접선도 쉽게 구할 수 있습니다.
q(w) = r + wr'
- 적분
- 곡선의 길이
곡선의 길이를 $l$이라 할때 곡선에서 $n$개의 선분들의 길이의 합을 극한 취하면 아래와 같은 정적분과 같이 됩니다.

- 호의 길이

곡선의 길이에서 나온 $l$의 값은 $a$, $b$의 값이 상수이기 때문에 $l$도 상수 입니다. 하지만 $b$의 값을 변수 $t$로 바꾸면 정적분에 관한 함수가 됩니다.

arc length 식을 미분하고 제곱하면
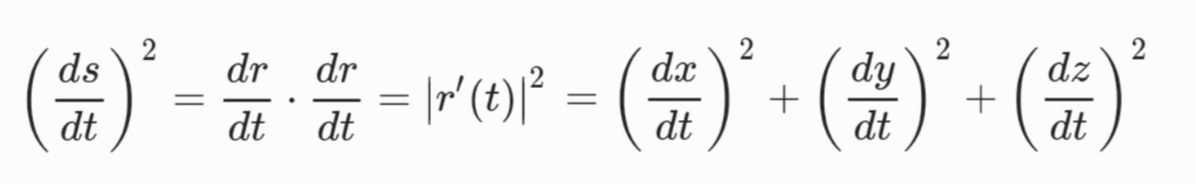
식을 얻을 수 있습니다.

▶ $ds$는 C의 선형요소(linear element) 라 부릅니다.
'수학 (Mathematics) > 공업 수학 (Advanced Engineering Mathematics)' 카테고리의 다른 글
| 스칼라장의 기울기 ( gradient ) (0) | 2020.03.13 |
|---|---|
| 벡터의 미적분 응용 (0) | 2020.03.13 |
| 벡터의 도함수 ( derivatives ) (0) | 2020.03.12 |
| 벡터의 외적 ( cross product ) (1) | 2020.03.11 |
| 벡터의 내적 (dot product) (0) | 2020.03.11 |




댓글